Computer Number System Conversions with Examples

 

Converting From One Number System to Another

 

Converting From Another Base to Decimal:

 

The following steps are used to convert a number in any other base to a base 10(decimal) number:

 

Step 1: Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).

 

Step 2: Multiply the obtained column values (in step 1) by the digits in the corresponding columns.

 

Step 3: Sum up the products calculated in step 2. The total is the equivalent value in decimal.

 

Ex 1:

 

4706₈=? ₁₀

 

Step 1: Determine the column values.

 

Column number (from right)	Column  value
1	80 = 1
2	81 = 8
3	82 = 64
4	83 = 512

 

 

Step 2: Multiply column values by the corresponding column digits.

 

512	64	8	1
x 4	x 7	x 0	x 6
2048	448	0	6

 

 

Step 3: Sum up the products

 

2048 + 448 + 0 + 6 = 2502

 

Hence, 4706₈= 2502₁₀

 

 

 

 

 

Ex 2:

 

1AC₁₆=? ₁₀

 

1AC₁₆ =1x16² + Ax16¹ + Cx16⁰

            =1x256 + 10x16 + 12x1

            = 256 + 160 +12

            = 428₁₀

 

Ex 3:

 

4052 ₇=? ₁₀

 

4052 ₇  = 4x7³ + 0x7² + 5x7¹ + 2x7⁰

            = 4x 343 + 0 x 49 + 5x7+ 2x1

            = 1372 + 0 + 35 + 2

            = 1409₁₀

 

Ex 4:

 

4052 ₆=? ₁₀

 

4052 ₆  = 4x6³ + 0x6² + 5x6¹ + 2x6⁰

            = 4x216 + 0x36 + 5x6 + 2x1

            = 864 + 0 + 30 + 2

            = 896₁₀

 

 

11001₄=? ₁₀   (Ans: 321₁₀)

 

1AC₁₃=? ₁₀     (Ans: 311₁₀)

 

 

Converting From Decimal to Another Base (Division Remainder Technique):

 

The following steps are used to convert a base 10(decimal) number to a number in another base:

 

Step 1: Divide the decimal number to be converted by the value of the new base.

Step 2: Record the remainder from Step 1 as the rightmost digit (least significant digit) of the new base number.

Step 3: Divide the quotient of the previous division by the new base.

Step 4: Record the remainder from Step 3 as the next digit (to the left) of the new base number.

 

Repeat Steps 3 and 4, recording remainders from right to left, until the quotient becomes zero in Step 3. Note that the last remainder thus obtained will be the most

significant digit (MSD) of the new base number.

Converting from a Base Other Than 10 to Another Base Other Than 10:

 

The following steps are used to convert a number in a base other than 10, to a number in another base other than 10:

 

Step 1: Convert the original number to a decimal number (base 10).

Step 2: Convert the decimal number so obtained to the new base number.

 

Examples:

Shortcut Method for Binary to Octal Conversion:

 

The following steps are used in this method:

 

Step 1: Divide the digits into groups of three starting from the right.

Step 2: Convert each group of three binary digits to one octal digit using the method of binary to decimal conversion.

 

Examples:

Shortcut Method for Octal to Binary Conversion:

 

Step 1: Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).

Step 2: Combine all the resulting binary groups (of 3 digits each) into a single binary number.

 

Examples:

Shortcut Method for Binary to Hexadecimal Conversion:

 

Step 1: Divide the binary digits into groups of four starting from the right.

Step 2: Combine each group of four binary digits to one hexadecimal digit.

 

Examples:

Shortcut Method for Hexadecimal to Binary Conversion:

 

Step 1: Convert the decimal equivalent of each hexadecimal digit to a 4 digit binary number.

Step 2: Combine all the resulting binary groups (of 4 digits each) in a single binary number.

 

Examples:

Fractional Numbers:

 

In binary number system, fractional numbers are formed in the same way as in a decimal number system. For example, in decimal number system,

 

0.235 = (2x10^-1) + (3x10^-2) + (5x10^-3) and

 

68.53 = (6x10¹) + (8x10⁰) + (5x10^-1) + (3x10^-2)

 

Similarly, in binary number system,

 

0.101 = (1x2^-1) + (0x2^-2) + (1x2^-3) and

 

10.01 = (1x2¹) + (0x2⁰) + (0x2^-1) + (1x2^-2)

 

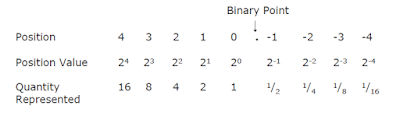
Hence, binary point serves the same purpose as decimal point. Some positional values in binary number system are given below.

In general, a number in a number system with base ‘b’ would be written as:

 

a_n a_n-1… a₀ . a_-1 a_-2 … a_-m

 

and would be interpreted to mean:

 

a_n x bⁿ + a_n-1 x b^n-1 + … + a₀ x b⁰ + a_-1 x b^-1 + a_-2 x b^-2 + … + a_-m x b^-m

 

The symbols a_n, a_n-1, …, a_-m in above representation should be one of the ‘b’ symbols allowed in the number system.

 

 

Examples: