OS Resource Allocation Graph (RAG)

 

Resource Allocation Graph (RAG):

 

Deadlocks can be described more precisely in terms of a directed graph called a system resource allocation graph. This graph consists of a set of vertices V and a set of edges E.

 

The set of vertices V  is partitioned into two different types of nodes P={P₁,P₂,...,P_n}, the set consisting of all the active processes in the system and R={R₁,R₂,...,R_m}  the set consisting of all the  resource types in the system.

 

A directed edge from process P_i to resource type R_j is denoted by P_i ->R_j.

 

It signifies that process Pi requested an instance of resource type R_j and is currently waiting for that resource.

 

A directed edge from resource type R_j to process P_i is denoted by R_j -> P_i.

 

It signifies that an instance of resource type R_j has been allocated to process P_i.

 

A directed edge P_i ->R_j is called a request edge, a directed edge R_j -> P_i is called an assignment edge.

 

Pictorially we represent each process P_i as a circle and each resource type R_j as a square. 

 

Since resource type R_j may have more than one instance we represent each such instance as a dot within the square.

 

A request edge points to only the square R_j where as an assignment edge must also designate one of the dots in the square.

 

When process P_i request an instance of resource type R_j a request edge is inserted into the resource allocation graph.

 

When this request can be fulfilled the request edge is instantaneously transformed to an assignment edge.

 

When the process no longer needs access to the resource it releases the resource and as a result the assignment edge is deleted.

 

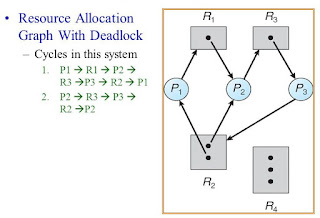
The Resource Allocation Graph depicts the following situation:

 

1.     The sets  P, R  and E;

a.    P={P₁,P₂,P₃}

b.    R={R₁,R₂,R₃,R₄}

c.    E={P₁->R₁,P₂->R₃,R₁->P₂, R₂->P₂,R₂->P₁,R₃->P₃}

           

2.  Resource instances:

a.    One instance of resource type R₁.

b.    Two instances of resource type R₂.

c.    One instance of resource type R₃.

d.    Three instances of resource type R₄.

 

3.    Process States:

a.    Process P₁ is holding an instance of resource type R₂ and is waiting for an instance of resource type R₁.

b.    Process P₂ is holding an instance of R₁ and R₂ and is waiting for an instance of resource type R₃.

c.    Process P₃ is holding an instance of R₃.

 

(Resource Allocation Graph)

(Resource Allocation Graph with deadlock)

(Resource Allocation Graph with cycle but no deadlock)

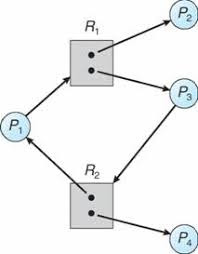
Given the definition of a resource allocation graph it can be shown that if the graph contains no cycles then no process in the system is deadlocked. If the graph does contain a cycle then a deadlock may exist.

 

If each resource type has exactly one instance then a cycle implies that a deadlock has occurred.

 

If the cycle involves only a set of resource types each of which has only a single instance then a deadlock has occurred. Each process involved in the cycle is deadlocked.  In this case a cycle in the graph is both a necessary and sufficient condition for the existence of deadlock.

 

If each resource type has several instances then a cycle does not necessarily imply that a deadlock has occurred.  In this case a cycle in the graph is a necessary but not a sufficient condition for the existence of deadlock.