Tabular Representation of Strong Entity, Weak Entity and Relationship Sets in DBMS

 

Tabular Representation of Strong Entity Sets:

 

Let ‘E’ be a strong entity set with descriptive attributes a₁, a_{2 . . .} a_n. We represent this entity by a table called E with ‘n’ distinct columns, each of which corresponds to one of the attributes of E. Each row in this table corresponds to one entity of the entity set E.

 

For ex: consider the entity set loan of the E-R diagram. It has two attributes: loan-number and amount. We represent this entity set by a table called loan, with two columns, as in below fig. We can add a new entity to the database by inserting a row into a table. We can also delete or modify rows.

 

Let D₁ denote the set of all loan numbers, and let D₂ denote the set of all balances. Any row of the loan table must consist of a 2-tuple (v₁, v₂), where v₁ is a loan (that is, v₁ is in set D₁) and v₂ is an amount (that is, v₂ is in set D₂). In general, the loan table will contain only a subset of the set of all possible rows.

 

We refer to the set of all possible rows of loan as the Cartesian product of D₁ and D₂, denoted by: D₁ × D₂

 

In general, if we have a table of ‘n’ columns, we denote the Cartesian product of D₁, D₂, · · ·D_n by: D₁ × D₂ × · · · × D_n−1 × D_n

Fig: Loan Table

Fig: Customer Table

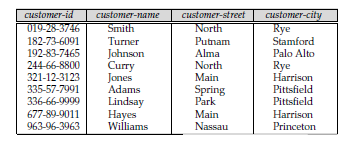
Consider another ex. of entity set customer having attributes customer-id, customer-name, customer-street, and customer-city. The table corresponding to the customer has four columns, as shown in above fig.

Tabular Representation of Weak Entity Sets:

 

Let ‘A’ be a weak entity set with attributes a₁, a₂ . . . , a_m. Let ‘B’ be the strong entity set on which ‘A’ depends. Let the primary key of ‘B’ consist of attributes b₁, b₂ . . . b_n. We represent the entity set ‘A’ by a table called ‘A’ with one column for each attribute of the set: {a₁, a₂ . . . a_m} ∪ {b₁, b₂ . . . b_n}

 

For ex: consider the entity set payment in the E-R diagram. This entity set has three attributes: payment-number, payment-date, and payment-amount. The primary key of the loan entity set, on which payment depends, is loan-number. Thus, we represent payment by a table with four columns labeled loan-number, payment-number, payment-date, and payment-amount, as shown in below fig.

Fig: Payment table

Tabular Representation of Relationship Sets:

 

Let ‘R’ be a relationship set, let a₁, a₂ . . . a_m be the set of attributes formed by the union of the primary keys of each of the entity sets participating in ‘R’, and let the descriptive attributes (if any) of ‘R’ be b₁, b₂ . . .  b_n. We represent this relationship set by a table called ‘R’ with one column for each attribute of the set:

{a₁, a₂ . . . a_m} ∪ {b₁, b₂ . . .  b_n}

 

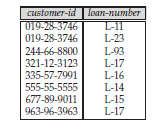
Consider the relationship set borrower in the E-R diagram. This relationship set involves the following two entity sets:

• customer, with the primary key customer-id

• loan, with the primary key loan-number

Since the relationship set has no attributes, the borrower table has two columns, labeled customer-id and loan-number, as shown in following fig.

Fig: Borrower table