Mapping Cardinalities or Types of Relationships in DBMS:

 

Mapping Cardinalities / Types of Relationships:

 

Mapping cardinalities or cardinality ratios express the number of entities to which another entity set can be associated via a relationship set. Mapping cardinalities are most useful in describing binary relationship sets, although they can contribute to the description of relationship sets that involve more than two entity sets.

 

For a binary relationship set R, between entity sets A and B, the mapping cardinality must be one of the following:

 

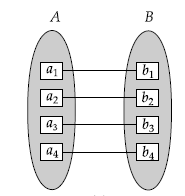
A.   One-to-One  (1:1) :

 

An entity in A is associated with at most one entity in B, and an entity in B is associated with at most one entity in A. Such a relationship is called as one to one relationship.

Fig: One to One relationship

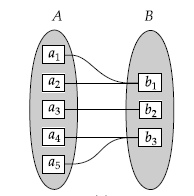
B.    One to Many(1:M) :

 

An entity in A is associated with any number (zero or more) of entities in B. An entity in B however, can be associated with at most one entity in A. Such a relationship is called as one to much relationship.

 

Fig: One to Many relationship

C.    Many to One(M:1):

 

An entity in A is associated with at most one entity in B. An entity in B however, can be associated with any number (zero or more) of entities in A. Such a relationship is called as many to one relationship.

Fig: Many to One relationship

For ex: consider the borrower relationship set. If in a particular bank a loan can belong to only one customer, and a customer can have several loans, then the relationship set from customer to loan is one to many.

D.    Many to Many(M:N):

 

An entity in A is associated with any number (zero or more) of entities in B, and an entity in B is associated with any number (zero or more) of entities in A. Such a relationship is called as many to many relationship.

Fig: Many to Many relationship

For ex: if a loan can belong to several customers (as loans is taken jointly by several business partners), the relationship set is many to many.